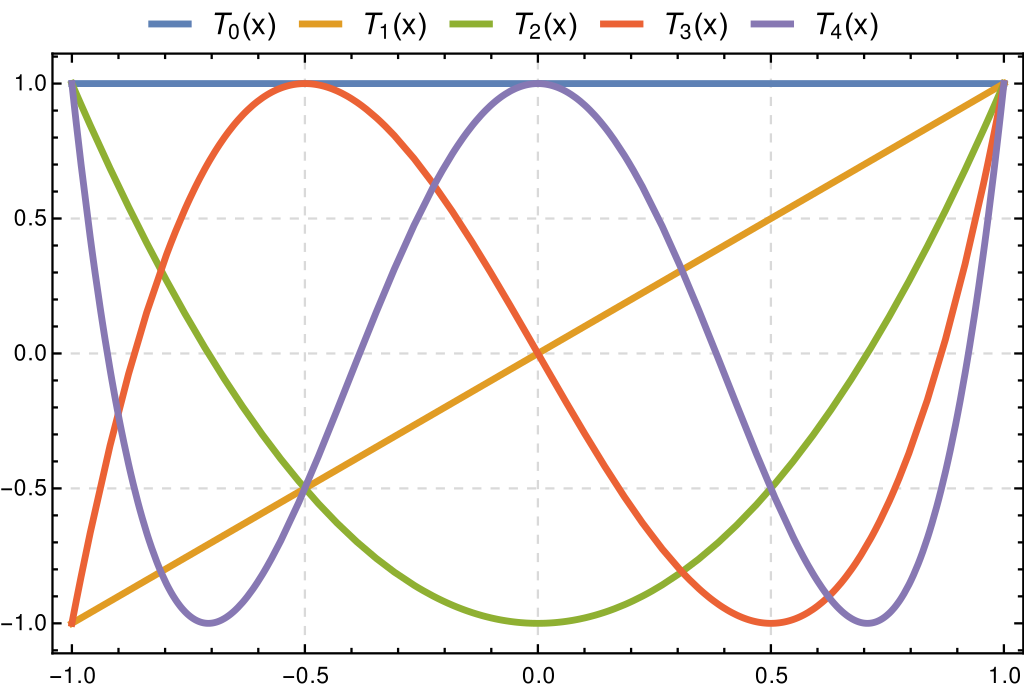
Tchebychev / Chebyshev functions and analysis

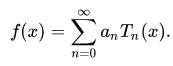
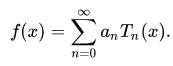
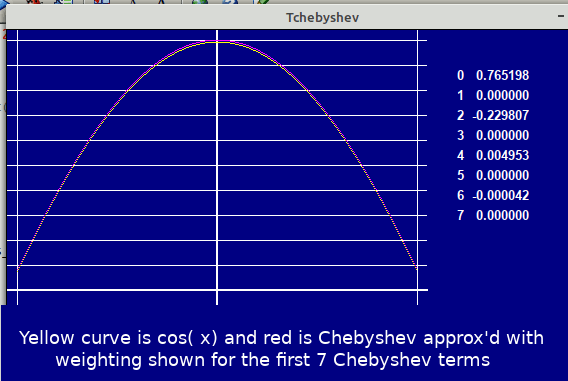
These are a set of functions that can be added, in different proportions, to synthesize a curve between two points. In this way they are like the Fourier addition of sin/cos terms to approximate the curve function. They are better approximations near the two end points, while Fourier is better if the sample curve is actually part of a repeating oscillating curve. ie 'The resulting interpolation polynomial minimizes the problem of Runge's phenomenon and provides an approximation that is closer to the polynomial of best approximation to a continuous function'.

Code for synthesising a cos curve

Red and yellow curves displaced by two pixels so visible.

Code

    nomainwin

    '   use only up to first 8 Tchebyshev terms ( 0 to 7)
    '   synthesises a cos curve between limits

    n       =200

    global pi: pi =4 *atn( 1)

    for c =0 to 7
        c( c) =0
        for k =0 to n
            xk      =cos( ( ( 2 *k +1) /(2 *( n +1))) *pi)

            if c =0 then
                c( c)   =c( c) +( 1 /( n +1)) *funcn( xk)
            else
                c( c)   =c( c) +( 2 /( n +1)) *funcn( xk) *Tchebyshev( c, xk)
            end if

        next k
        'print using( "##.####", c( c))
    next c

    print

    WindowWidth  =640
    WindowHeight =460
6
    open "Tchebyshev" for graphics_nsb as #wg

    #wg "trapclose quit"

    #wg "down ; fill darkblue"
    #wg "color white"

    for h =0 to 9 step 0.5
        if h =5 then #wg "size 2" else #wg "size 1"
        #wg "up ; goto  0 "; 10 +50 *h; " ; down ; goto 420 "; 10 +50 *h
    next h

    for v =0 to 2
        if v =1 then #wg "size 2" else #wg "size 1"
        #wg "up ; goto "; 10 +200 *v; " 0 ; down ; goto "; 10 +200 *v; " 420"
    next v

    for x =-1 to 1 step 0.005
        print using( "##.##", x), using( "##.####",funcn( x)),
        #wg "color 255 255 0 ; set "; int( ( x +1) *200 +10); " "; int( 512 -funcn( x) *500)
        t =0
        for c =0 to 7
            t =t +c( c) *Tchebyshev( c, x)
        next c
        print using( "##.####", t)
        #wg "color 255 0 255 ; set "; int( ( x +1) *200 +10); " "; int( 510 -t *500)
    next x

    #wg "color white ; backcolor darkblue"

    for i =0 to 7
        #wg "up ; goto 450 "; 50 +i *20
        #wg "down"
        #wg "\"; i; "  "; using( "##.######", c( i))
    next i

    wait'_____________________________________________________________________

    function Tchebyshev( n, x)
        select case
            case x >1
                Tchebyshev =cosh( n *arcCosh( x))
            case x <-1
                Tchebyshev =cos(  n *arcCosh( x))
            case ( ( x >=-1) and ( x <=1))
                Tchebyshev =cos(  n *acs(     x))
        end select
    end function

    function cosh( x)
        cosh    =0.5 *( exp( x) +exp( 0 -x))
    end function

    function arcCosh( x)
        if x >1 then arcCosh =log( x +( x^2 -1)^0.5)
    end function

    sub quit h$
        close #wg
        end
    end sub

    sub delay t
        timer t *1000, [o]
        wait
        [o]
        timer 0
    end sub

    function funcn( x)
        funcn =cos( x)
        'funcn4 *sin( x)^2
        'funcn =exp( x)  '   1.2661  1.1302  0.2715  0.0443 is expected
        'funcn =4 *x^2
        'funcn =4 *sin( pi *x)
    end function

Code for analysing a curve to find Chebyshev amplitudes

Finding coefficient weightings.


    WindowWidth  = 550
    WindowHeight = 400

    graphicbox #w.gb1, 10,  10, 520, 220
    graphicbox #w.gb2, 10, 240, 520, 100

    nomainwin

    global terms
    terms =50   '100  '20   '150   '150

    dim weighting( terms)

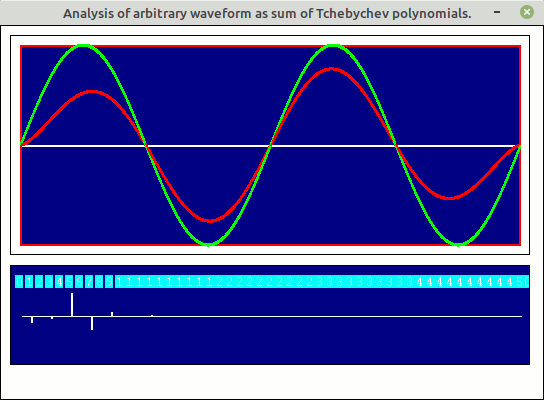
    open "Analysis of arbitrary waveform as sum of Tchebychev polynomials." for graphics_nsb_nf as #w

    #w "trapclose [quit]"

    #w.gb1 "size 2 ; color red"
    #w.gb1 "up ; goto 10 210 ; down ; backcolor darkblue ; boxfilled 510 10"
    #w.gb1 "up ; goto 10 110 ; down ; color white ; goto 510 110 ; color red"

    #w.gb2 "goto 510 50 ; down ; fill darkblue ; color white ; goto 10 50 ; color darkblue ; backcolor cyan"

    for x =-1 to 1 step 0.002
        for tch =0 to terms
            weighting( tch) =weighting( tch) +fn( x) *tchebychev( tch, x) /1000
        next tch
    next x

    #w.gb2 "font courier "; str$( int( 3 +terms /30)); " ; color white"
    for x =0 to terms
        #w.gb2 "up ;  goto "; 10 +x /terms *500; " "; 50 -weighting( x) *50
        #w.gb2 "down; boxfilled "; 10 +x /terms *500 +100 /terms; " "; 50
        #w.gb2 "up ; goto "; 4 +x /terms *500; " "; 20
        #w.gb2 "down"
        #w.gb2 "|"; x
    next x

    for x =-1 to 1 step 0.002
        #w.gb1 "color red ;   set "; 10 +( x +1) /2 *500; " "; 110 -100 *sumTerms( x)    '   tchebychev( n, x)
        #w.gb1 "color green ; set "; 10 +( x +1) /2 *500; " "; 110 -100 *fn( x)
    next x

    #w.gb1 "flush"
    #w.gb2 "flush"
    wait

[quit]
    close #w
    end

function tchebychev( n, x)
    if abs( x) >1 then end
    tchebychev =cos( n *acs( x))
end function

function sumTerms( x)
    s =0
    for j =0 to terms
        s =s +weighting( j) *tchebychev( j, x)
    next j
    sumTerms =s
end function

function fn( x)
    'if x <0 then fn =0 -0.5 -x else fn =0 -0.5 +x
    'if x <0 then fn =-1 else fn =1
    fn =sin( 2 *3.14159265 *x)
    'fn =cos( 2 *3.14159265 *x)
    'fn =x
    'fn =0.5
    'fn =x^2
end function