Population modelling- the Lotke/Volterra equations.

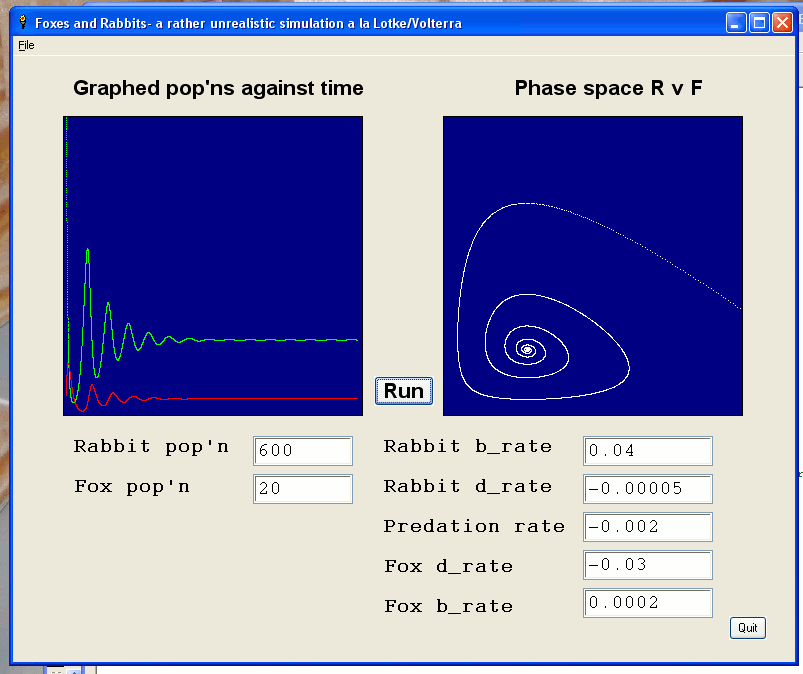
The situation of rabbits ( feeding off inexhaustible grass) and foxes ( feeding off rabbits) is simulated with two differential equations, ie the change in a next SHORT interval is calculated from the present values. Rabbit birth rate is fixed, ie double the population means it increases twice as fast. They die depending on the frequency of encountering a fox, ie proportionally to the product of the two populations. Foxes have a fixed death rate, but breeding again depends on successful feeding, so is proportional to the population product. You can add a rabbit-limiting effect with a term depending on crowding, ie rabbits squared.

Solutions are shown as two population/time graphs; and as a 'rabbit/fox phase space' diagram, which emphasises the cyclical nature.

Solutions should repeat, cyclically, but often seem to show cycles which increase or decrease unboundedly, as above. This means you have to reduce dt and accept slower solutions, because if each step makes more than a tiny change in r or f population, the result will be in error if the gradient is changing quickly. Mind you, the erroneous patterns look pretty, even if they have no correspondence to reality!

The later versions of the simulation allow you to change dt to limit this error.

There are many improvements that could be made to make it all more realistic. And things like range-checking and auto scaling and axis labelling should be improved. Some day...

The following code needs two bitmaps, available in the zipped package.


    '   **************************************
    '   EcoCK1.bas   tenochtitlanuk  Dec. 2010
    '   **************************************

    '   To-dos:-
    '       Check for overflows
    '       Add display of end state, ie # of Rs & Fs.
    '       Add x and y scales to graphs.
    '       Add a screensave/ print.
    '       Bring in greater realism!
    '   ......................................


    UpperLeftX   =  10
    UpperLeftY   =  10
    WindowWidth  = 790
    WindowHeight = 660

    nomainwin

    R   = 100.0
    F   =  20.0

    A   =   0.04
    B   =  0'-0.00005
    C   =  -0.002
    D   =  -0.03
    E   =   0.0002

    graphicbox #m.gb1,  50,  60, 300, 300
    graphicbox #m.gb2, 430,  60, 300, 300

    statictext #m.st1, "",  60,  20, 700,  30
    statictext #m.st2, "", 370, 380, 200, 300
    statictext #m.st3, "",  60, 380, 180, 300

    button #m.b1, "Run",  [DoRun], LR, 395, 260, 60, 30
    button #m.b2, "Quit", [quit],  LR,  40,  20

    textbox #m.tb1, 570, 380, 130, 30
    textbox #m.tb2, 570, 418, 130, 30
    textbox #m.tb3, 570, 456, 130, 30
    textbox #m.tb4, 570, 494, 130, 30
    textbox #m.tb5, 570, 532, 130, 30

    textbox #m.tb6, 240, 380, 100, 30
    textbox #m.tb7, 240, 418, 100, 30

    textbox #m.tb8, 240, 494, 100, 30

    menu    #m, "&File", "&Help", [Help], |, "Exit", [quit]

    cr$  =chr$( 13)
    dt   =1  '   Set step forward small enough for lines to look continuous...

    open "Foxes and Rabbits- a rather unrealistic simulation a la Lotke/Volterra" for window as #m

    #m "trapclose [quit]"

    #m.st1 "!font arial 16 bold"
    #m.st1 "Graphed pop'ns against time                         Phase space R v F"

    #m.tb1 "!font courier 16"
    #m.tb2 "!font courier 16"
    #m.tb3 "!font courier 16"
    #m.tb4 "!font courier 16"
    #m.tb5 "!font courier 16"
    #m.tb6 "!font courier 16"
    #m.tb7 "!font courier 16"
    #m.tb8 "!font courier 16"

    #m.b1 "!font arial 16 bold"

    #m.tb1 A
    #m.tb2 B
    #m.tb3 C
    #m.tb4 D
    #m.tb5 E
    #m.tb6 R
    #m.tb7 F
    #m.tb8 dt

    #m.st2 "!font courier 16 bold"
    #m.st3 "!font courier 16 bold"

    #m.st2 "Rabbit b_rate"; cr$; cr$; "Rabbit d_rate"; cr$; cr$; "Predation rate"; cr$; cr$; "Fox d_rate"; cr$; cr$; "Fox b_rate"
    #m.st3 "Rabbit pop'n"; cr$; cr$; "Fox pop'n"; cr$; cr$; cr$; cr$; "Time step."

    loadbmp "LH", "LH.bmp"
    loadbmp "RH", "RH.bmp"
    #m.gb1 "down ; drawbmp LH 0 0 ; flush"
    #m.gb2 "down ; drawbmp RH 0 0 ; flush ; color cyan"
    unloadbmp "RH"
    unloadbmp "LH"

    wait

  [DoRun]
    i = 0

    #m.gb1 "cls ; fill darkblue"
    #m.gb2 "cls ; fill darkblue ; color cyan"

    #m.tb1 "!contents? v$": A  =val( v$)
    #m.tb2 "!contents? v$": B  =val( v$)
    #m.tb3 "!contents? v$": C  =val( v$)
    #m.tb4 "!contents? v$": D  =val( v$)
    #m.tb5 "!contents? v$": E  =val( v$)
    #m.tb6 "!contents? v$": R  =val( v$)
    #m.tb7 "!contents? v$": F  =val( v$)
    #m.tb8 "!contents? v$": dt =val( v$)

    do
        Rchange    =  dt *( A *R                           +B *R^2                                     +C *R *F)
        ' Births prop'l to pop'n.       Deaths prop'l crowding (pop'n squared)        and predation prop'l to encounters.

        Fchange    =  dt *( D *F                                                           +E *R *F)
        ' Deaths prop'l to fox population.            Births prop'l to population times food availability/encounters.

        #m.gb1 "color green"
        #m.gb1 "set " ; 2 +i /10 *dt; " " ; 298 -R /2

        #m.gb1 "color red"
        #m.gb1 "set " ; 2 +i /10 *dt; " " ; 298 -F

        #m.gb2 "set " ; R /1.8; " "; 298 -F *4

        R =R +Rchange
        F =F +Fchange

        print " R= "; R, "F= "; F

        i      =i +1

        scan

    loop until ( i >3000 /dt) or ( R <=0) or ( F <=0)

    #m.gb1 "flush"
    #m.gb2 "flush"

    wait

[Help]
    statictext #p.st "", 10, 10, 580, 480
    WindowWidth  =605
    WindowHeight =505

    open "Population dynamics- brief explanation of the simulation." for dialog_nf_modal as #p

    #p "trapclose [close2]"
    #p.st "!font arial 12"
    #p.st cr$; "      *****    This simulates foxes preying on rabbits.      ******"; cr$; cr$;_
    " The rabbits feed on inexhaustible grass."; cr$;_
    " Rabbits have a birth rate that is fixed, but crowding increases their death rate"; cr$;_
    "       because their greater density makes predation easier,"; cr$;_
    "       as does an increased number of foxes!"; cr$; cr$;_
    " Foxes have fixed birth/death rates, but increase faster if there are more rabbits."; cr$; cr$;_
    " You can play with the constants involved."; cr$; cr$;_
    " Results are generally cyclic. You alter all parameters."; cr$; cr$;_
    " Lack of realism includes absence of effects like- no alternative foods;"; cr$;_
    "       other competing species; saturation of fox appetite; evolution;"; cr$;_
    "       random climate changes"; cr$; cr$;_
    " Extreme cases include initial start with zero of either population!"; cr$; cr$;_
    " Always adjust dt downward until not expanding or contracting noticeably...."; cr$; cr$;_
    " NB There are no range or graph-scale checks...."
    wait

    [close2]
    close #p

[quit]
    close #m
    end

E-mail me on mr.john.f at gmail.com if you have problems...