Perceptrons
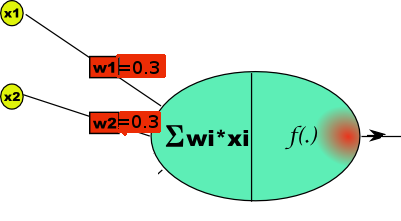

A 'neuron' is a cell/circuit that takes one or more inputs, each with different sensitivity/importance. If the weighted sum of these inputs exceeds a threshold, the cell fires/is activated. The human brain is believed to contain wetware involving 10^10 such cells...
The weighting was done by motor-driven potentiometers, which held the weight value even if switched off. Learning involved adjusting the weights until the perceptron had learned the desired function.
The original machine had a whole array of say 20x20 CdS photocells in a grid, onto which were projected, say, coarse-resolution images of letters of the alphabet. 26 perceptrons, each with a random selection of the 400 inputs but different weights, could then 'learn' the alphabet. That's 400 photocells/amplifiers, and up to 26 *400 motor driven potentiometers. See Wikipedia
Unfortunately, it was soon proved that perceptrons would never be able to create certain selected output functions. Specifically, they could learn logic gating like AND or OR, but not XOR!
In the learning phase, the various binary input possibilities are presented, and the output with the present weights is compared with the desired output. Specifically, we sum the product of input values times weight of that path/input, and see if the sum exceeds the threshold. The weights are immediately corrected by an amount depending on their present value, the corresponding input, and a fixed 'learning rate'. The set of inputs is repeatedly presented until the weights converge on values which predict correctly.
In the operation phasenew inputs are presented and the circuit/code gives the correct output.
In some languages, eg Python, there are neat ways to represent variable-length lists/vectors, and do things like dot-product ( sum the product of each term in one list ( representing the inputs) multiplied by the corresponding one in another list ( representing the corresponding weights).
In LB you can do this kind of operation with arrays, but for a general implementation it's a pain deciding what dimension to give the arrays and not waste space. I instead used the 'word$(' operator to concatenate lists.
weights$ = "0.0,0.0,0.0" represents a list of three weights, each initialized to 0.0.
trainingSet$ = "1,0,0,;0 1,0,1,;0 1,1,0,;0 1,1,1,;1" represents a list of lists. Its first term, '1,0,0,;0', represents three inputs, '1,0,0' and the desired output, '0'.
threshold = 0.5
learningRate = 0.1
global nInputs
' Rem/Unrem any one of the following, which all work.
trainingSet$ = "0,0,;0 0,1,;0 1,0,;0 1,1,;1" ' AND list/vector of 4 (sub-) list/vectors rep'g 3 inputs and desired output
'trainingSet$ = "1,0,0,;0 1,0,1,;0 1,1,0,;0 1,1,1,;1" ' AND list/vector of 4 (sub-) list/vectors rep'g 3 inputs and desired output
'trainingSet$ = "1,0,0,;0 1,0,1,;1 1,1,0,;1 1,1,1,;1" ' OR list/vector of 4 (sub-) list/vectors rep'g 3 inputs and desired output
'trainingSet$ = "1,0,0,;1 1,0,1,;1 1,1,0,;1 1,1,1,;0" ' NAND list/vector of 4 (sub-) list/vectors rep'g 3 inputs and desired output
'trainingSet$ = "1,0,0,;0 1,0,1,;0 1,1,0,;0 1,1,1,;0" ' NONE list/vector of 4 (sub-) list/vectors rep'g 3 inputs and desired output
'trainingSet$ = "1,0,0,;1 1,0,1,;1 1,1,0,;1 1,1,1,;1" ' ANY list/vector of 4 (sub-) list/vectors rep'g 3 inputs and desired output
'trainingSet$ = "0,0,0,;0 0,0,1,;0 0,1,0,;0 0,1,1,;0 1,0,0,;0 1,0,1,;0 1,1,0,;0 1,1,1,;1" ' AND list/vector of 4 (sub-) list/vectors rep'g 3 inputs and desired output
'trainingSet$ = "1,0,0,;0 1,0,1,;1 1,1,0,;1 1,1,1,;0" ' XOR list/vector of 4 (sub-) list/vectors rep'g 3 inputs and desired output
' NB the failure to be able to learn XOR led to the decades of 'AI Famine'.
' then it was realised multi-layer perceptrons CAN learn this and other symmetric examples.
tests = count( trainingSet$, " ") +1: print " Num. test cases supplied, with desired output-", tests
case1$ = word$( trainingSet$, 1, " "): print " First case supplies- ",,, case1$
nInputs = count( case1$, ","): print " Number of input signal paths- ",, nInputs: print ""
for i = 1 to nInputs
weights$ = weights$ +"0.0"
if i <> nInputs then weights$ = weights$ +","
next i 'weights$ is a single list/vector, representing synapse weights
for jj =1 to 20
scan
for i = 1 to tests
trainer$ = word$( trainingSet$, i, " ") ' eg 1,0,0,;1
p = instr( trainer$, ";")
signal$ = left$( trainer$, p - 2)
desiredOutput = val( word$( trainer$, 2, ";")) ' eg 1
'print "We want "; signal$; " to produce "; desiredOutput
dotProduct = 0
for ii = 1 to nInputs
w = val( word$( weights$, ii, ","))
v = val( word$( signal$, ii, ","))
'print w; " * "; v;
'if ii <3 then print " + "; else print " = ";
dotProduct = dotProduct + w * v
next ii
'print " dotProduct of "; dotProduct
'print " .... so error = ";
if dotProduct > threshold then result = 1 else result = 0
er = desiredOutput - result
' print er
if er <> 0 then
w1 = val( word$( weights$, 1, ",")) + learningRate * er * val( word$( signal$, 1, ","))
w2 = val( word$( weights$, 2, ",")) + learningRate * er * val( word$( signal$, 2, ","))
w3 = val( word$( weights$, 3, ",")) + learningRate * er * val( word$( signal$, 3, ","))
weights$ = str$( w1) + "," +str$( w2) + "," +str$( w3)
end if
call pprint weights$
print ""
next i
print ""
next jj
print " Test whether it works, after learning from examples."
for i =1 to tests
read tv$
tv$ = right$( tv$, 2 * nInputs -1)
o = 0
for k =1 to nInputs
o = o +val( word$( tv$, k, ",")) *val( word$( weights$, k, ","))
next k
print " "; tv$,
if o < threshold then print 0 else print 1
next i
end
'data "0,0,0", "0,0,1", "0,1,0", "0,1,1", "1,0,0", "1,0,1", "1,1,0", "1,1,1"
data "1,1,1", "1,1,0", "1,0,1", "1,0,0", "0,1,1", "0,1,0", "0,0,1", "0,0,0"
sub pprint i$
for i =1 to nInputs
print using( "###.###", val( word$( i$, i, ","))),
next i
end sub
function count( t$, c$)
count =0
for i = 1 to len( t$)
if mid$( t$, i, 1) = c$ then count =count + 1
next i
end function
trainingSet$ = "0,0,;0 0,1,;0 1,0,;0 1,1,;1" ' AND
It generates the weights shown-
0.300 0.300
. . . . . and demonstrates it working-
Test whether it works, after learning from examples. 1,1 1 1,0 0 0,1 0 0,0 0
. . . . . which is indeed an AND function. No input, or only one, total 0 or 0.3 and are below 0.5 threshold. Two inputs total 0.6 and exceed it...
