Hyperbolic functions

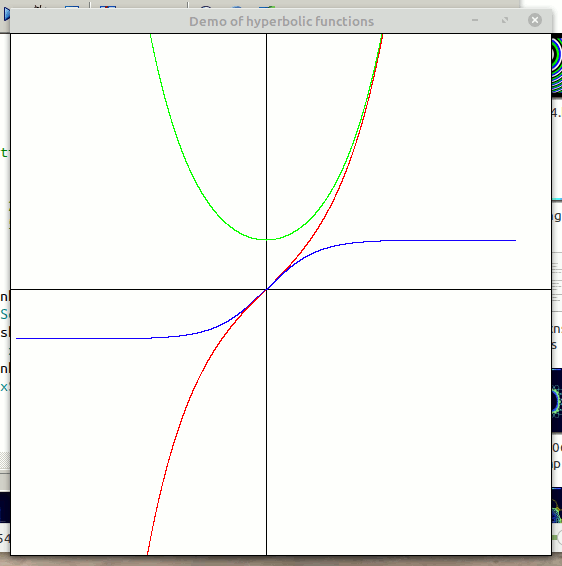
In nature, represent the shape of a rope hung from to places- the 'catenary'.

Code

    nomainwin

    WindowWidth  =550
    WindowHeight =550

    open "Demo of hyperbolic functions" for graphics_nsb as #gw

    #gw "trapclose quit"
    #gw "goto 255 0 ; down ; goto 255 550 ; up"
    #gw "goto 0 255 ; down ; goto 550 255"

    for x =-5 to 5 step 0.001
        xScreen =255 +x *50
        yScreen =255 -int( 50 *sinh( x))
        #gw "color red ; set "; xScreen; " "; yScreen
        yScreen =255 -int( 50 *cosh( x))
        #gw "color green ; set "; xScreen; " "; yScreen
        yScreen =255 -int( 50 *tanh( x))
        #gw "color blue ; set "; xScreen; " "; yScreen
    next x

    #gw "getbmp scr 1 1 550 550"
    bmpsave "scr", "hyperbolics.bmp"
    wait

    end

    sub quit h$
        close #gw
        end
    end sub

    function sinh( x)
        sinh =( 1 -exp( 0 -2 *x)) /( 2 *exp( 0 -x))
    end function

    function cosh( x)
        cosh =( 1 +exp( 0 -2 *x)) /( 2 * exp( 0 -x))
    end function

    function tanh( x)
        tanh =( 1 -exp( 0 -2 *x)) /( 1 + exp( 0 -2 *x))
    end function