Towers of Hanoi

This is a classic logic problem, fun to program graphically and particularly fun on a real physical set-up. Mine is wooden.

A novice takes time to solve it, given the rules that you can only..

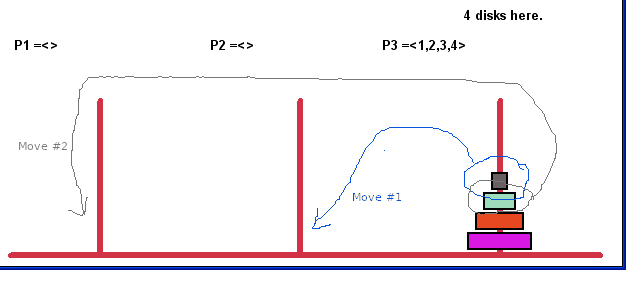
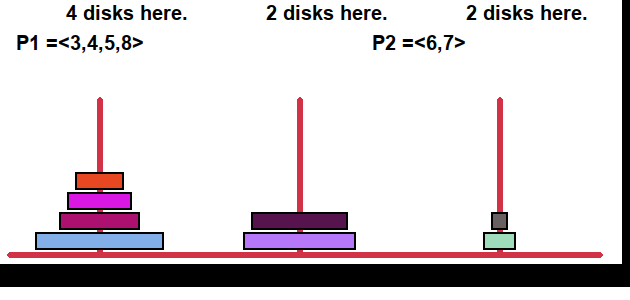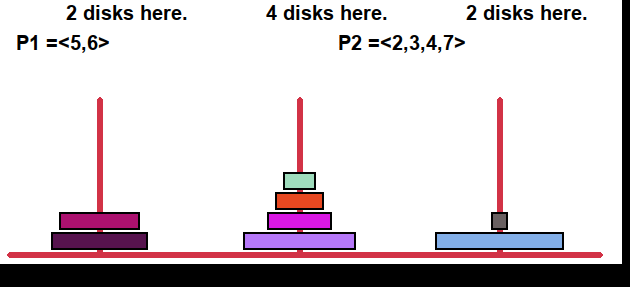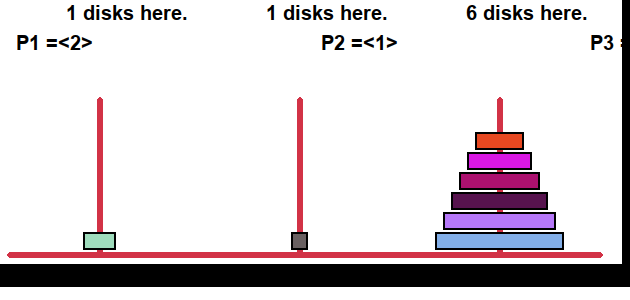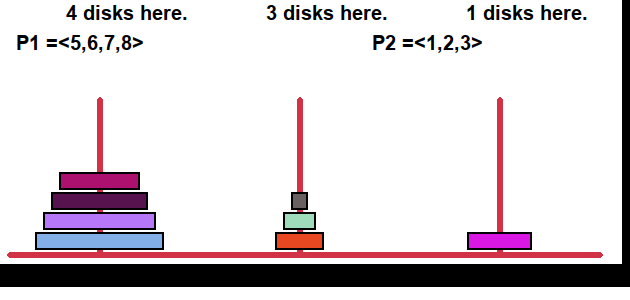
However there is a simple solution a novice can be taught in seconds that makes them able to solve it quickly with next to no thought. For the 8 disks shown below you can do it in 256 moves.

    '   **** Recursive Hanoi with GUI *****

    nomainwin

    global N, c
    N =8    '   NB stay below 10...
    c =1
    
    for i =1 to N   '   load peg 1
        peg$( 1) =peg$( 1) +str$( i)
        if i <>N then peg$( 1) =peg$( 1) +","
    next i

    peg$( 2) =""
    peg$( 3) =""

    source$ ="A"
    via$    ="B"
    target$ ="C"

    for i =0 to N
        color$( i) =str$( int( 256 *rnd( 1))) +" " +str$( int( 256 *rnd( 1))) +" " +str$( int( 256 *rnd( 1)))
    next i

    WindowWidth  =630
    WindowHeight =300

    open "Towers of Hanoi- recursively" for graphics_nsb_nf as #w

    #w "trapclose quit"
    #w "down"

    call hanoi N, source$, target$, via$
    call display

    wait

    sub hanoi numDisks, source$, target$, via$
        if numDisks =0 then
            exit sub
        else
            call hanoi numDisks -1, source$,   via$,      target$
            print
            print " Peg A =# "; peg$( 1); " #"; tab( 20);  "Peg B =# "; peg$( 2); " #"; tab( 40); "Peg C =# "; peg$( 3); " #"
            print " Move disk "; numDisks; " from peg "; source$; " to peg "; target$
            call display

            beingMoved$ =""

            select case source$
                case "A"
                    beingMoved$ =word$( peg$( 1), 1, ",")
                    if len( peg$( 1)) <>1 then peg$( 1) =mid$( peg$( 1), instr( peg$( 1), ",") +1) else peg$( 1) =""    '   loses LH term & it is held in beingMoved$
                case "B"
                    beingMoved$ =word$( peg$( 2), 1, ",")
                    if len( peg$( 2)) <>1  then peg$( 2) =mid$( peg$( 2), instr( peg$( 2), ",") +1) else peg$( 2) =""
                case "C"
                    beingMoved$ =word$( peg$( 3), 1, ",")
                    if len( peg$( 3)) <>1  then peg$( 3) =mid$( peg$( 3), instr( peg$( 3), ",") +1) else peg$( 3) =""
            end select

            select case target$
                case "A"
                    if peg$( 1) ="" then peg$( 1) =beingMoved$ else peg$( 1) =beingMoved$ +"," +peg$( 1)  '   gains LH term previously held in beingMoved$
                case "B"
                    if peg$( 2) ="" then peg$( 2) =beingMoved$ else peg$( 2) =beingMoved$ +"," +peg$( 2)
                case "C"
                    if peg$( 3) ="" then peg$( 3) =beingMoved$ else peg$( 3) =beingMoved$ +"," +peg$( 3)
            end select

            call hanoi numDisks -1, via$,      target$,   source$
        end if
        end sub

        sub display '   display a disk stack described as say "1,2,3" on peg 1
        #w "cls"

        #w "color 210  50  70"
        #w "place  10 255 ; size 6 ; goto 600 255"
        #w "place 100 255 ; goto 100 100"
        #w "place 300 255 ; goto 300 100"
        #w "place 500 255 ; goto 500 100"

        #w "color black"

        #w "size 2 ; backcolor white"
        #w "place 10 50"
        #w "\ P1 =<"; peg$( 1); ">                                      P2 =<"; peg$( 2); ">                                P3 =<"; peg$( 3); ">"
        for peg =1 to 3   '   draw the disks specified at the three peg positions
            if len( peg$( peg)) <>0 then
                numDisksHere =0
                for i =1 to len( peg$( peg))
                    if mid$( peg$( peg), i, 1) ="," then numDisksHere =numDisksHere +1
                next i
                numDisksHere =numDisksHere +1
                #w "backcolor white"
                #w "place "; 60 +200 *( peg -1); " 20"
                #w "\ "; numDisksHere; " disks here."
                for i =0 to numDisksHere -1
                    w =val( word$( peg$( peg), numDisksHere -i, ","))
                    #w "backcolor "; color$( w)
                    #w "place ";     peg *200 -w *8 -100; " "; 250 +( 0 -i) *20
                    #w "boxfilled "; peg *200 +w *8 -100; " "; 250 +( 0 -i) *20 -17

                next i
            end if
        next peg
        #w "backcolor white"
        '#w "flush"
        '#w "getbmp scr 0 0 630 300"
        'bmpsave "scr", "hanoi"; c; ".bmp"
        'c =c +1
        'unloadbmp "scr"
        'timer 100, [p]
        'wait
      '[p]
        'timer 0
    end sub

sub quit a$
    close #a$
    end
end sub