Original inspiration- from 1978.

Could I reproduce this graphic? Circles and spirals are easy, but I'd never drawn arcs. Was it even a genuine computer picture- 1978 meant computer graphics available to amateurs were primitive. Perhaps a spirograph contraption? I put it on the LB Forum as a challenge and Rod, Anatoly and Bplus produced excellent efforts.

See Liberty BASIC Forum.

Given two points and a circle-centre there are four arc solutions in two mirror-image pairs.

The geometry is basically right-angle triangles and trig. It still took some time before I was happy with my own solutions. Then I realised there were already solutions on Rosetta Code...

I now concentrated on fun USING arcs, and hope to come up with further variations. I use HSV colouring to get results I find pleasing.

Code of one demonstration.

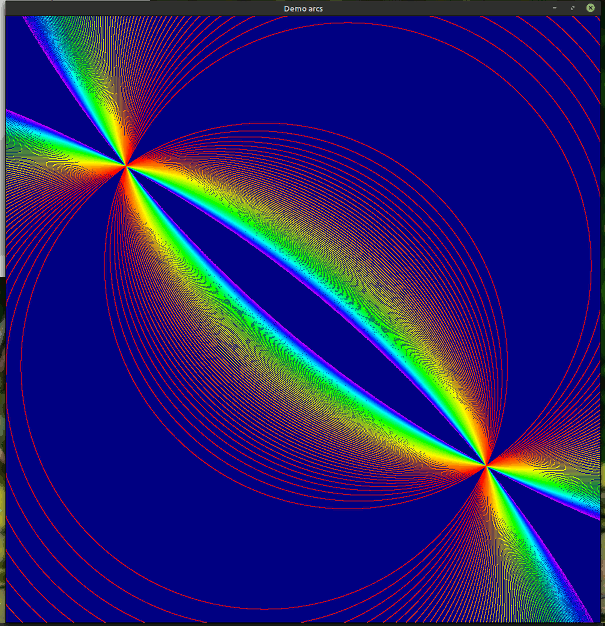
    '[RC] Circles of given radius through two points

    nomainwin

    global col$, pi, state$
    pi =atn( 1) *4

    WindowWidth  =1000
    WindowHeight =1040

    open "Demo arcs" for graphics_nsb as #wg

    #wg "trapclose quit"

    #wg "fill darkblue ; color 100 255 255"

    radius =2000
    x1     = 200
    y1     = 250
    x2     = 800
    y2     = 750

    #wg "up ; goto "; x1; " "; y1
    #wg "down ; circle 4"
    #wg "up ; goto "; x2; " "; y2
    #wg "down ; circle 4 ; flush"

  [H]
    call twoCircles x1, y1,    x2, y2,      radius
    scan
    radius =radius *0.98
    if radius >400 then [H]

    #wg "flush ; getbmp scr 0 0 1000 1040"
    bmpsave "scr", "arcs.bmp"
    notice "arcs2.bmp saved"

    wait

    sub quit h$
        close #wg
        end
    end sub

    sub  twoCircles  x1, y1,     x2, y2,     r
        if ( ( x1 =x2) and ( y1 =y2)) or ( r =0) then wait  '   single point or radius zero!
        r2      =( ( x1 -x2)^2 +( y1 -y2)^2)^0.5 /2         '   half distance between points
        if r one revolution
        x   =c *( 1 -abs( ( ( h /60) mod 2) -1))
        m   =v -c   '                               matching adjustment

        select case
            case h < 60
                r = c: g = x: b = 0
            case h <120
                r = x: g = c: b = 0
            case h <180
                r = 0: g = c: b = x
            case h <240
                r = 0: g = x: b = c
            case h <300
                r = x: g = 0: b = c
            case else
                r = c: g = 0: b = x
        end select

        rd      = abs( int( 256 *( r + m)))
        gn      = abs( int( 256 *( g + m)))
        bu      = abs( int( 256 *( b + m))) '   NB csv version .. <<<<<<<<<<<<<<<<<<<<<<<<<<
        col$    =right$( "  " +str$( rd), 3) +" " +right$( "   " +str$( gn), 3) +" " +right$( "   " +str$( bu), 3)

    end sub

    function ATAN2( y, x)
        Result$ = "Undetermined"
        If ( x =0) and ( y >0) then ATAN2 = pi /2:      Result$ ="Determined"
        if ( x =0) and ( y <0) then ATAN2 =3 * pi /2:   Result$ ="Determined"
        if ( x >0) and ( y =0) then ATAN2 =0:           Result$ ="Determined"
        if ( x <0) and ( y =0) then ATAN2 =pi:          Result$ ="Determined"

        If Result$ <>"Determined" then
            BaseAngle =ATN( abs( y) /abs( x))
            If ( x >0) and ( y >0) then ATAN2 =        BaseAngle
            If ( x <0) and ( y >0) then ATAN2 = pi    -BaseAngle
            If ( x <0) and ( y <0) then ATAN2 = pi    +BaseAngle
            If ( x >0) and ( y <0) then ATAN2 = 2 *pi -BaseAngle
        end if
    End Function

    function cosRad( t)
        cosRad =cos( t /57.29577951)
    end function

    function sinRad( t)
        sinRad =sin( t /57.29577951)
    end function