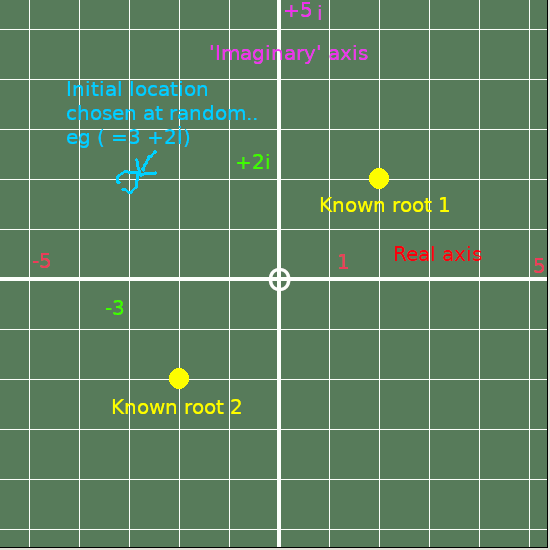
but COMPLEX as well as REAL..
If we consider polynomials in x eg f( x) =x^2 -3x +2, we see that it has 'roots' at x =1 and x =2, where f( x) =0.
To find an EXACT root when it happens not to be a nice integer we can draw a nice curve by hand, but much better is to use Newton's method, which basically says make any guess, then a better one will be found by following the tangent at the first guess back to the f( x) =0 axis. This is met in very early calculus class. Basically
x --> x =f( x) /f'( x)
ie replace the guess by its value minus the result of dividing f( x) value at the guess by f'( x) there, where the prime sign ' means first derivative or gradient.
I first coded this a decade or so back in LB.
I've also coded things like Mandelbrots, but Ray brough me back to the Newton Method- but with it generalised to polynomials which have complex roots as well or in place of real ones.
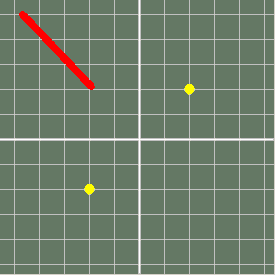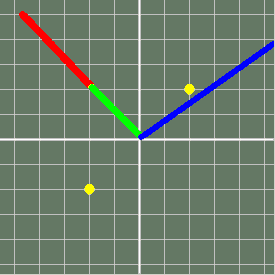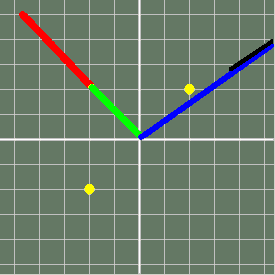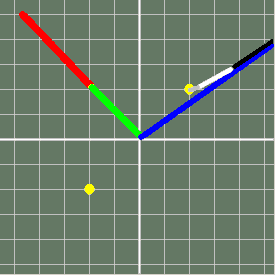
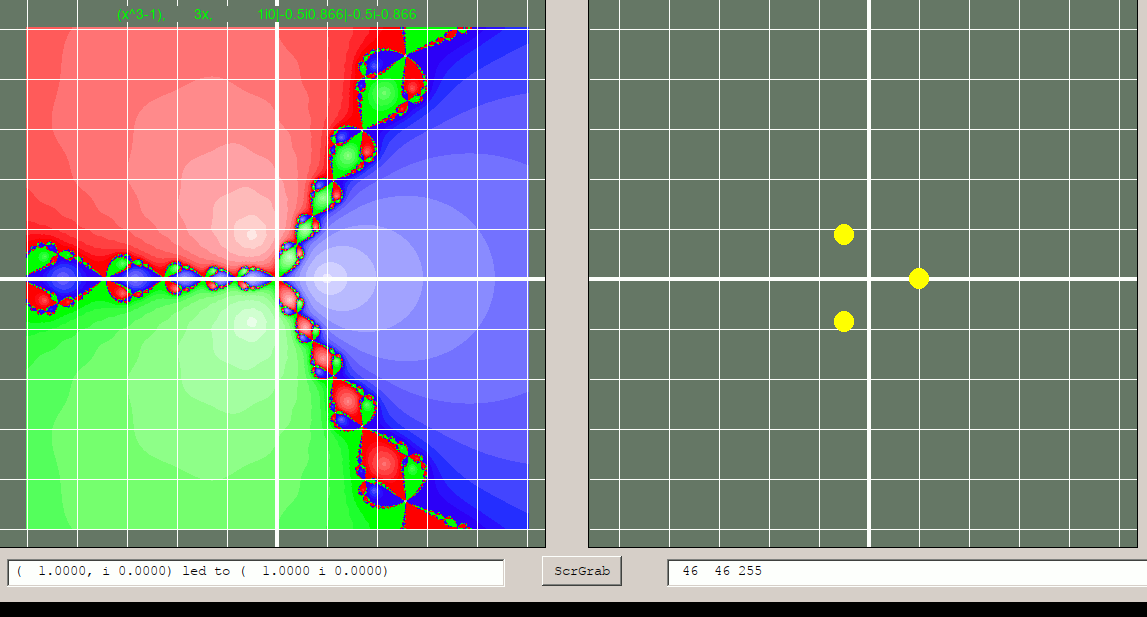
The diagram shows that you can choose ANY point in the complex plane, apply Newton's method, and in the great majority of cases you will converge to one of the possible roots ( occasionally yoou might get an oscillation instead).

The following show the path followed in several cases...
Start near a root- gets there in three steps..
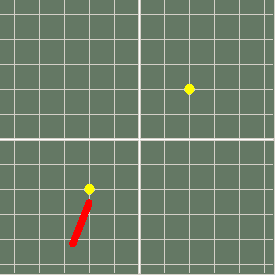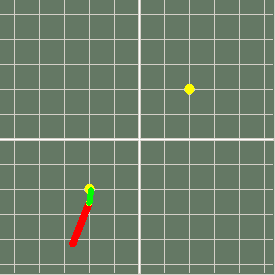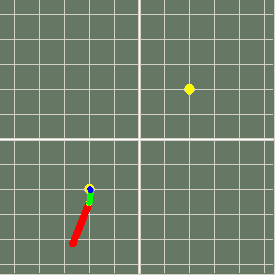
Further from a root- takes seven steps

Zig-zags pretty wildly but gets there...
Another fairly weird path..

Each step is basically a rotation and displacement, applied repeatedly. The further you are from a root the longer it will take to get to the root. And there must be a borderline where a tiny difference in start position could send you to one ot to another root.. hence we bring in fractal behaviour.
If we systematically try all points in the range of interest ( or Monte Carlo fashion, try them all in random order) we can colour code them for which root they ended at. Even better, we can modulate the colour saturation to represent the number of iterations it took.
Unfortunately LB does not have complex numbers and arithmetic operations on them. I wrote some years ago however. And it will be VERY slow. To explore to 2 decimal places all possible starting points between -5 and +5 on real and imaginary axes means 500 *500 starting points, typically iterating 3 to 15 times at each, and with the overhead of my routines, Definitely 'go have a coffee' time, but worth it for the nice graphics. Next improvement is to add the ability to zoom into the fractal areas- they have infinite level of detail!
This page is provisional- code is being developed further and will be added/altered soon. Or PM me...
' **********************************************************************************************************
' ************* Format representing a complex number is a string. "2i-2" is ( 2 -2i) ***************
' ************* ***************
' ************* Supply 'roots' and the polynomial f( x) and derivative f'( x) ***************
' ************* Draw the fate of iterations from all starting points in the mapped area ***************
' ************* ***************
' ************* testRootsInvd7.bas July 2109 tenochtitlanuk ***************
' ************* ***************
' **********************************************************************************************************
' Version to save bursts of typical root seeking iterations...
' to-do's
' add on-screen display of f(x) and routes done
' add save or print screen- save added
' routine to zoom
' routine to plot a dot at start for the given roots done
' move the division to ( corrected) proc 'cDivision('
' trap and debug the divide-by-zero error OK
' 'exit for' if within 'eps' of a root done
' use number of iterations to fade the root colour done
' test with eg f( x) =x^2 -i *x -2 *i, roots 2 and -i, f'( x) =2 *x -i current
' add button to screengrab on demand EDIT to grab an iteration sequence
global p: p =0 ' <<<<<<<<<<<<<<<<<<< for use in drawing iteration route...
allCol$ ="red,green,blue,yellow,lightgray,black,white,lightgray,brown,pink,darkcyan,darkgreen,darkred"
nomainwin
'on error goto [errorHandler]
global delta, type$, m, dist
type$ ="gt-" ' ie graphics, text, both, and with w.g2 suppressed.
firstTime =0
UpperLeftX = 4: UpperLeftY = 4
WindowWidth =1180: WindowHeight =660
textbox #w.tb, 20,580, 500, 30
textbox #w.tb2, 680,580, 500, 30
graphicbox #w.g, 10, 20, 550, 550
graphicbox #w.g2, 602, 20, 550, 550
button #w.b1, "ScrGrab", scr, LR, 590, 20, 80, 30
open "Complex plane- Newton Fractals" for window as #w
#w "trapclose quit"
#w.g "down ; fill 100 120 100"
#w.g2 "down ; fill 100 120 100 ; flush ; color white"
#w "font Courier_New 7"
gosub [grid]
#w.g "flush"
' word$( 1) =f(x), word$( 2) =f'( x), word$( 3) solutions sep'd by '|'.
' f(x), f'(x), root( 1)| root( 2)|...etc
command$ ="(x+2i2)(x-2i-2) OR x^2 -8i, 2x, 2i2|-2i-2"
w$ =word$( command$, 3, ",")
a1$ =word$( w$, 1, "|")
a2$ =word$( w$, 2, "|")
'a3$ =word$( w$, 3, "|")
a1R$ =word$( a1$, 1, "i"): a1I$ =word$( a1$, 2, "i")
a2R$ =word$( a2$, 1, "i"): a2I$ =word$( a2$, 2, "i")
'a3R$ =word$( a3$, 1, "i"): a3I$ =word$( a3$, 2, "i")
R( 1) =val( a1R$): I( 1) =val( a1I$) ' R( n) and I( n) hold real and imaginary parts of roots
R( 2) =val( a2R$): I( 2) =val( a2I$) ' add further roots if polynomial is above quadratic
'R( 3) =val( a3R$): I( 3) =val( a3I$)
delta =0.2
delta =max( 0.02, delta)
eps =0.0001
'while 1
'x =-5 +delta *int( 10 /delta *rnd(1)) ' use for Monte Carlo runs
'y =-5 +delta *int( 10 /delta *rnd(1))
'scan
for x =( 0 -5 -delta /2) to ( 5 +delta /2) step delta
for y =-5 to ( 5 +delta /2) step delta
x$ =str$( x) +"i" +str$( y) ' start at random place in complex ( Real/Imaginary) plane
h$ =x$ ' hold initial start location while x$ iterates..
sR =x: sI =y ' hold previous position on iteration path
gosub [grid2]
'#w.g2 "getbmp scr 1 1 550 550": bmpsave "scr", str$( x) +"_" +str$( y) +"_itern_" +str$(m ) +"_" +str$( time$( "seconds")) +".bmp":wait
'if instr( type$, "-") =0 then
#w.g2 "up ; goto "; 280 +int( sR *50); " "; 280 -int( sI *50)
'end if
for m =0 to 12 ' twelve iterations normally plenty '
topLine$ =cAdd$( cSqu$( x$), "0i-8")
bottomLine$ =cProd$( x$, "2i0")
' multiply top and bottom by complex-conjugate of bottom line to make bottom line real..
CC$ =cConj$( bottomLine$)
topLine$ =cProd$( topLine$, CC$)
bottomLine$ =cProd$( bottomLine$, CC$)
divBy =val( word$( bottomLine$, 1, "i"))
if divBy =0 then exit for
presentR =val( word$( topLine$, 1, "i"))
presentI =val( word$( topLine$, 2, "i"))
R =presentR /divBy
I =presentI /divBy
if abs( R) >1000 then exit for
if abs( I) >1000 then exit for
x$ =cSub$( x$, str$( R) +"i" +str$( I)) ' calculates new approximation
R =val( word$( x$, 1, "i")) ' x --> x -f( x) /f'( x)
I =val( word$( x$, 2, "i"))
if ( abs( R) 0 then #w.g2 "getbmp scr 1 1 550 550": bmpsave "scr", str$( x) +"_" +str$( y) +"_itern_" +str$(m ) +"_" +str$( time$( "seconds")) +".bmp"
next m
'if instr( type$, "t") then #w.tb2 "..hopped to...( "; using( "##.####", sR); ", i";_
' using( "##.####", sI); ")"
'gosub [grid2]
'if p <>0 then #w.g2 "getbmp scr 1 1 550 550": bmpsave "scr", str$( x) +"_" +str$( y) +"_itern" +str$( time$( "seconds")) +".bmp"
if p<>0 then p =0
scan
R =val( word$( x$, 1, "i"))
I =val( word$( x$, 2, "i"))
' find distance of current end point ( R, I) from each root ( R( n), I( n)) ...
' NB add to if >quadratic..<<
dist1 =( ( R -R( 1))^2 +( I -I( 1))^2)^0.5
dist2 =( ( R -R( 2))^2 +( I -I( 2))^2)^0.5
'dist3 =( ( R -R( 3))^2 +( I -I( 3))^2)^0.5
#w.g "backcolor cyan ; color cyan ; down"
m =min( m, 11)
m$ =right$( " " +str$( int( ( 11 -m) /11 *255)), 3)
red$ ="255 " +m$ +" " +m$
green$ =m$ +" 255 " +m$
blue$ =m$ +" " +m$ +" 255"
if dist1 0 and firstTime <> 1 then
#w.g2 "cls ; fill 100 120 100"
#w.g2 "color white" ' subroutine to draw grid and roots
for x2 =-5 to 5
if x2 =0 then #w.g2 "size 4" else #w.g2 "size 1"
#w.g2 "up ; goto "; 280 +x2 *50; " 0 ; down ; goto "; 280 +x2 *50; " 600"
next x2
for y2 =-5 to 5
if y2 =0 then #w.g2 "size 4" else #w.g2 "size 1"
#w.g2 "up ; goto "; 570; " "; 280 +y2 *50; " ; down ; goto 0 "; 280 +y2 *50
next y2
#w.g2 "size 20 ; color yellow ; down"
#w.g2 "set "; 280 -50 *2; " "; 280 +50 *2
#w.g2 "set "; 280 +50 *2; " "; 280 -50 *2
'#w.g2 "set "; 280 +50 *0; " "; 280 +50 *1
#w.g2 "size 1"
'end if
firstTime =1
return
[grid]
#w.g "color white" ' subroutine to draw grid and roots
for x =-5 to 5
if x =0 then #w.g "size 4" else #w.g "size 1"
#w.g "up ; goto "; 280 +x *50; " 0 ; down ; goto "; 280 +x *50; " 600"
next x
for y =-5 to 5
if y =0 then #w.g "size 4" else #w.g "size 1"
#w.g "up ; goto "; 570; " "; 280 +y *50; " ; down ; goto 0 "; 280 +y *50
next y
#w.g "size 20 ; color yellow ; down"
if instr( type$, "-") =0 then
#w.g2 "set "; 280 -50 *2; " "; 280 +50 *2
#w.g2 "set "; 280 +50 *2; " "; 280 -50 *2
'#w.g2 "set "; 280 +50 *0; " "; 280 +50 *1
end if
#w.g "size 1"
return
sub quit h$
close #w
end
end sub
end
sub scr h$
'#w.g "up ; goto 120 20 ; down ; color green ; backcolor 100 120 100 ; font 7"
'#w.g "\"; command$
'#w.g "flush"
'#w.g "getbmp scr 1 1 1200 650"
'bmpsave "scr", "test4.bmp"
p =1
end sub
[errorHandler]
print "Error string is " + chr$(34) + Err$ + chr$(34)
print "Error number is ";Err
end
' Collection of functions of a complex number a$ expressed in 'real i imag' ...
' cAdd$( a$, b$)
' cSub$( a$, b$)
' cConj$( a$)
' cProd$( a$, b$)
' cSqu$( a$)
' cCube$( a$)
' check( a$)
' cDiv( a$, b$)
' cPrint(
' a$ uses global selector "t"|"g"|"gt" for text only, graphics only or both
function i$( k$)
R =val( word$( k$, 1, "i"))
I =val( word$( k$, 2, "i"))
tmp =I
I =R
R =0 -tmp
i$ =str$( R) +"i" +str$( I)
end function
function cConj$( I$)
R =val( word$( I$, 1, "i"))
I =val( word$( I$, 2, "i"))
I =0 -I
cConj$ =str$( R) +"i" +str$( I)
end function
function cSqu$( i$)
cSqu$ =cProd$( i$, i$)
end function
function cCube$( i$)
cCube$ =cProd$( i$, cSqu$( i$))
end function
function check( c$)
check =0
sepPosn =instr( c$, "i")
select case
case sepPosn =0
print " Malformed c number! No 'i'.": check =1
case str$( val( word$( c$, 1, "i"))) <>word$( c$, 1, "i")
print " Malformed c number! Number error in real part.": check =2
case str$( val( word$( c$, 2, "i"))) <>word$( c$, 2, "i")
print " Malformed c number! Number error in imaginary part.": check =3
end select
end function
function cDiv$( a$, b$) ' <<<<< TBC <<<<<<<<<<<<<<<<
' multiply top and bottom by c conjugate of denominator ( denominator becomes a pure real) and calculate.
aR =val( word$( a$, 1, "i")): aI =val( word$( a$, 2, "i"))
CC$ =cConj$( b$)
CCR =val( word$( CC$, 1, "i")): CCI =val( word$( CC$, 2, "i"))
if ( abs( CCR) <1e6) and ( abs( CCI) >1e-6) then
R =aR /CCR
I =aI /CCR
else
R =1E6
Y =1E6
end if
cDiv$ =str$( R) +"i" +str$( I)
end function
function cProd$( a$, b$)
aR =val( word$( a$, 1, "i")): aI =val( word$( a$, 2, "i"))
bR =val( word$( b$, 1, "i")): bI =val( word$( b$, 2, "i"))
R =aR *bR -aI *bI
I =aR *bI +aI *bR
cProd$ =str$( R) +"i" +str$( I)
end function
function cAdd$( a$, b$)
aR =val( word$( a$, 1, "i")): aI =val( word$( a$, 2, "i"))
bR =val( word$( b$, 1, "i")): bI =val( word$( b$, 2, "i"))
R =aR +bR
I =aI +bI
cAdd$ =str$( R) +"i" +str$( I)
end function
function cSub$( a$, b$)
aR =val( word$( a$, 1, "i")): aI =val( word$( a$, 2, "i"))
bR =val( word$( b$, 1, "i")): bI =val( word$( b$, 2, "i"))
R =aR -bR
I =aI -bI
cSub$ =str$( R) +"i" +str$( I)
end function