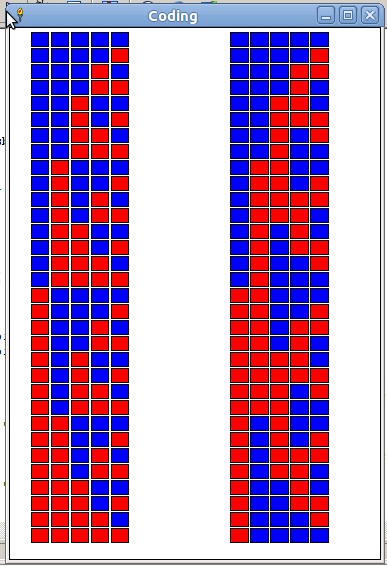
When contact or opto sensors are used to sense linear or angular position, pure binary suffers from the disadvantage that a slightly misaligned sensor can give a reading which is wildly wron, since if only one bit is read from the neighbouring number bit-pattern rather than the correct one, it can alter the result by 2^n-1, ie in 8-bit numbers, by 2^7. To avoid this disaster, Gray code is used. Here, adjacent codes differ by only ONE bit, so a misread bit either makes NO difference, or only +/-1.

For a rotary encoder you'd wrap the above pattern round a cylinder, or re-map it to a circle.
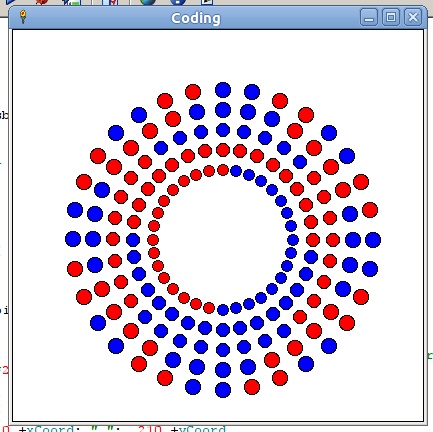
Variations of the below code were used to draw the graphic representations used here. It is also easy to print out a table of values, or call the functions from your own code.
0 00000 00000 00000 1 00001 00001 00001 2 00010 00011 00010 3 00011 00010 00011 4 00100 00110 00100 5 00101 00111 00101 6 00110 00101 00110 7 00111 00100 00111 8 01000 01100 01000 9 01001 01101 01001 10 01010 01111 01010 11 01011 01110 01011 12 01100 01010 01100 13 01101 01011 01101 14 01110 01001 01110 15 01111 01000 01111 16 10000 11000 10000 17 10001 11001 10001 18 10010 11011 10010 19 10011 11010 10011 20 10100 11110 10100 21 10101 11111 10101 22 10110 11101 10110 23 10111 11100 10111 24 11000 10100 11000 25 11001 10101 11001 26 11010 10111 11010 27 11011 10110 11011 28 11100 10010 11100 29 11101 10011 11101 30 11110 10001 11110 31 11111 10000 11111 Decimal 23 is 10111 in binary, & 11100 in Gray code.
mainwin 100 20
print
print " Some examples of decimal, binary & Gray code conversion."
print
for i =1 to 10
r =int( 500 *rnd( 1))
print " Decimal "; using( "###", r); " is '";
print dec2Bin$( r); "' in binary, & '";
print Bin2Gray$( dec2Bin$( r)); "' in Gray code."
next i
print
print " bin2Dec( '11110000')"; " is "; bin2Dec( "11110000")
print " dec2Bin$( 46) is '"; dec2Bin$( 46); "'"
end
function dec2Bin$( num) ' Given an integer decimal, returns binary equivalent as a string
n =num
dec2Bin$ =""
while ( num >0)
dec2Bin$ =str$( num mod 2) +dec2Bin$
num =int( num /2)
wend
if ( n >255) then nBits =16 else nBits =8
dec2Bin$ =right$( "0000000000000000" +dec2Bin$, nBits) ' Pad to 8 bit or 16 bit
end function
function bin2Dec( b$) ' Given a binary number as a string, returns decimal equivalent num.
t =0
d =len( b$)
for k =d to 1 step -1
t =t +val( mid$( b$, k, 1)) *2^( d -k)
next k
bin2Dec =t
end function
function Bin2Gray$( bin$) ' Given a binary number as a string, returns Gray code as a string.
g$ =left$( bin$, 1)
for i =2 to len( bin$)
bitA =val( mid$( bin$, i -1, 1))
bitB =val( mid$( bin$, i, 1))
AXorB =bitA xor bitB
g$ =g$ +str$( AXorB)
next i
Bin2Gray$ =g$
end function
function Gray2Bin$( g$) ' Given a Gray code as a string, returns equivalent binary num. as a string
gl =len( g$) ' NB calculating a Gray code of numbers over 256 is a bit silly...
b$ =left$( g$, 1) ' But I was too lazy to put in any checks!!
for i =2 to len( g$)
bitA =val( mid$( b$, i -1, 1))
bitB =val( mid$( g$, i, 1))
AXorB =bitA xor bitB
b$ =b$ +str$( AXorB)
next i
Gray2Bin$ =right$( b$, gl)
end function