Example of 2D projectile.
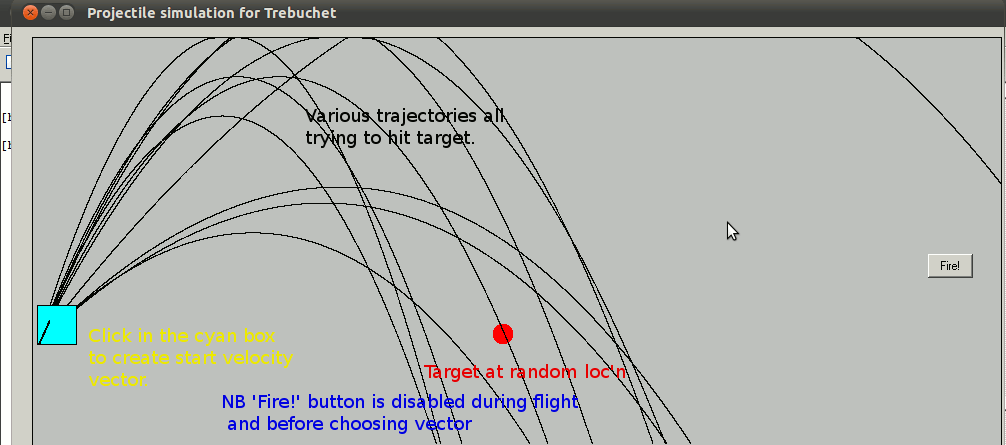

The screenshot shows a demonstration of code to model projectile flight in two dimensions. You are presented with a randomly-positioned target, and can use the mouse left-click in the little aiming box to set direction and speed of the discharge. Vertical motion experiences gravity and air drag; horizontally it meets only air drag.
When you've set the velocity, click 'Fire!'.
As set up, it leaves a trace of the track. You could instead move a sprite.....
You can easily change parameters like 'g', mass, cross sectional area and friction coefficient. It also can be easily made to loop through a family of curves.

You could easily add a routine to check if you made a 'Hit' and add scoring, etc.
The following code runs in Liberty or Just BASIC.
' *************************************************
' ** **
' ** Trebuchet4.bas **
' ** **
' *************************************************
' ** tenochtitlanuk ( John F) Feb. 2011 **
' Investigating real-world projectile motion.
' Allows you to play with 2D motion in g-field
' Includes effect of air friction.
' You can alter initial velocity and angle.
' To-dos:-
' Add dialogue boxes to change the variables.
' Add option of a target to hit.
nomainwin
UpperLeftX = 10
UpperLeftY = 10
WindowWidth =1000
WindowHeight = 680
graphicbox #w.g2, 25, 278, 40, 40
graphicbox #w.g, 20, 10, 970, 610
button #w.b1, "Fire!", [here], LR, 50, 400
statictext #w.st1, "Initialise", 20, 630, 550, 20
open "Projectile simulation for Trebuchet" for window as #w
#w, "trapclose [quit]"
#w.g2 "when leftButtonDown [vector]"
#w.g, "cls ; size 2 ; color red "
#w.g "down ; fill lightgray"
#w.g "up ; goto "; 400 +400 *rnd( 1); " "; 305 -200 *rnd( 1)
#w.g "down ; backcolor red ; circlefilled 10"
#w.g "up ; goto 5 305 ; color darkblue"
#w.g "down ; goto 985 305 ; color black ; size 1 ; down ; flush"
#w.g2 "size 2 ; down ; fill cyan ; flush"
m = 1 ' fixed mass of stone in kg.
A = 0.002 ' csa of stone in m^2.
g = 9.81 ' acc'n of gravity m^s2.
D = 1.2 ' density of air.
Cd = 0.75 ' allows for the shape.
v = 60 ' release velocity in m/s.
theta = 30 ' release angle in degrees,
theta =theta /180 *3.14159265 ' ... changed to radians.
y = 0 ' initial vertical height.
vy = v *cos( theta) ' initial vertical vel'y.
x = 0 ' initial horizontal position.
vx = v *sin( theta) ' initial horizontal vel'y.
t = 0 ' initial time. s
dt = 0.001 ' time interval between updates.
wait
[here]
#w.b1 "!disable"
[h]
fy =0 -g *m -0.5 *D *vy^2 *Cd *A *sgn( vy)
ay =fy /m
vy =vy +ay *dt
y =y +vy *dt
fx =0 -0.5 *D *vx^2 *Cd *A *sgn( vx)
ax =fx /m
vx =vx +ax *dt
x =x +vx *dt
t =t +dt
#w.g, "set "; 5 +2.5 *x; " "; 305 -2.5 *y
scan
if x <400 and y >-40 then [h]
#w.g "flush"
#w.b1 "!enable"
wait
[vector]
x =0
y =0
xx =MouseX
yy =MouseY
#w.g2 "cls ; down ; fill cyan ; up ; goto 0 39 ; down ; goto "; xx; " "; yy
theta =atn( ( 39 -yy) /xx)
v =2 *( xx^2 +( 39-yy)^2)^0.5
#w.st1 "v ="; using( "###.#", v); " & angle ="; using( "###.#", theta *180 /3.14159265); " degrees."
vy = v *sin( theta) ' initial vertical vel'y.
vx = v *cos( theta) ' initial horizontal vel'y.
wait
function sgn( x)
if x <0 then
sgn =-1
else
sgn = 1
end if
end function 'sgn
[quit]
close #w
end
' *************************************************
' ** **
' ** Trebuchet7.bas **
' ** **
' *************************************************
' ** tenochtitlanuk ( John F) Feb. 2011 **
' Investigating real-world projectile motion.
' Allows you to play with 2D motion in g-field
' Includes effect of air friction.
' You can alter initial velocity and angle.
' To-dos:-
' Move graphics vertically done
' Add dialogue boxes to change the variables.
' possibly use cursor keys to tweak...
' Add option of a target to hit. done
' Add a score based on time taken to hit target?
' Score near-misses as well as hits. (air bursts)
nomainwin
UpperLeftX = 10
UpperLeftY = 10
WindowWidth =1000
WindowHeight = 680
graphicbox #w.g2, 25, 465, 100, 100
stylebits #w.g2, 0, _WS_BORDER, 0, 0
graphicbox #w.g, 20, 10, 970, 610
button #w.b1, "Fire!", [here], LR, 940, 50
statictext #w.st1, "Initialise", 20, 630, 550, 20
open "Projectile simulation for Trebuchet" for window as #w
#w, "trapclose [quit]"
#w.g2 "when leftButtonDown [vector]"
#w.g2 "when characterInput [here]"
#w.g, "cls ; size 2 ; color red "
#w.g "down ; fill darkgray"
xt =100 +250 *rnd( 1)
yt =200 -200 *rnd( 1)
#w.g "up ; goto "; 5 +2.5 *xt; " "; 555 -2.5 *yt
#w.g "down ; backcolor red ; circlefilled 10"
#w.g "up ; goto 5 555 ; color darkblue"
#w.g "down ; goto 985 555 ; color black ; size 1 ; down ; flush"
#w.g2 "size 3 ; down ; fill cyan ; color lightgray ; box 99 99 ; flush ; color black"
m = 1 ' fixed mass of stone in kg.
A = 0.005 ' csa of stone in m^2. More like 0.002
g = 9.81 ' acc'n of gravity m^s2.
D = 1.2 ' density of air.
Cd = 2 ' allows for the shape. Correct value =0.75??
v = 60 ' release velocity in m/s.
theta = 30 ' release angle in degrees,
theta = theta /180*3.14159265 ' ... changed to radians.
y = 0 ' initial vertical height.
vy = v *cos( theta) ' initial vertical vel'y.
x = 0 ' initial horizontal position.
vx = v *sin( theta) ' initial horizontal vel'y.
t = 0 ' initial time. s
dt = 0.004 ' time interval between updates.
wait
[here]
#w.b1 "!disable"
#w.g "color "; 256 *rnd( 1); " "; 256 *rnd( 1); " "; 256 *rnd( 1)
[h]
fy =0 -g *m -0.5 *D *vy^2 *Cd *A *sgn( vy)
ay =fy /m
vy =vy +ay *dt
y =y +vy *dt
fx =0 -0.5 *D *vx^2 *Cd *A *sgn( vx)
ax =fx /m
vx =vx +ax *dt
x =x +vx *dt
t =t +dt
#w.g, "set "; 5 +2.5 *x; " "; 555 -2.5 *y
proximity =( xt -x)^2 +( yt -y)^2
if proximity <400 *4 /25 then #w.g "color yellow" else #w.g "color black"
scan
if x <400 and y >-40 then [h]
#w.g "flush"
#w.b1 "!enable"
wait
[vector]
x =0
y =0
xx =MouseX
yy =MouseY
#w.g2 "cls ; down ; fill darkgray ; up ; goto 0 99 ; down ; goto "; xx; " "; yy
theta =atn( ( 99 -yy) /xx)
v =( xx^2 +( 99-yy)^2)^0.5
#w.st1 "v ="; using( "###.#", v); " & angle ="; using( "###.#", theta *180 /3.14159265); " degrees."
vy = v *sin( theta) ' initial vertical vel'y.
vx = v *cos( theta) ' initial horizontal vel'y.
#w.b1 "!enable"
wait
function sgn( x)
if x <0 then
sgn =-1
else
sgn = 1
end if
end function 'sgn
[quit]
close #w
end