Strange result in last digits of primes.

Evelyn Lamb and Scientific American drew my attention to the recently announced observation that if you consider the last digit of each successive prime number ( which must be a 1, 3, 7 or 9 after the first 2 and 5) then it 'avoids' the last digit of the previous prime.

Any mathematician /programmer immediately tries coding it to see this improbable result.

The original discoverers checked a billion digits. My code checks far fewer ( 360,000 or 1,000,000)!

Give the code time- it does a 'Sieve of Eratosthenes' first, displayed graphically on-screen...

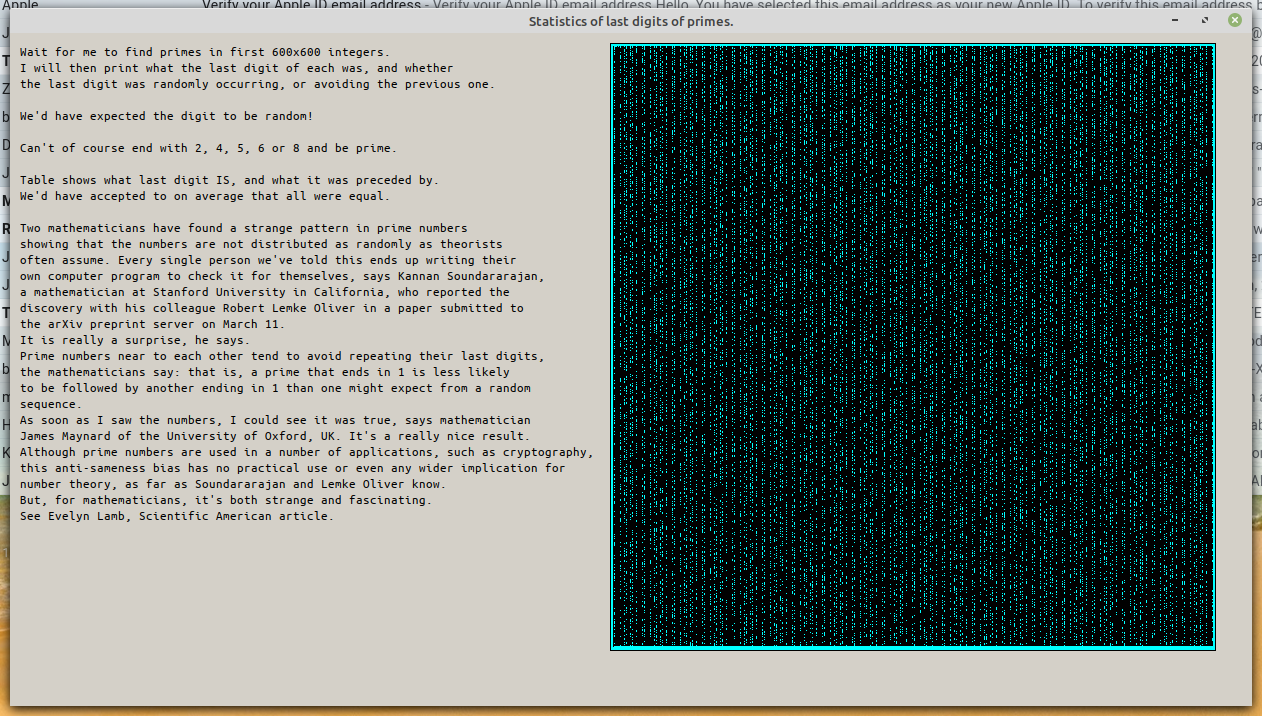
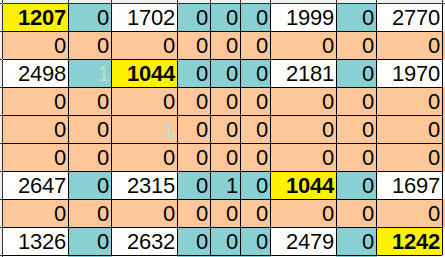
Note how say '1' followed by '1' is far less common than '1' followed by any of '3, 7 or 9'.

Now to investigate how far down-the-line this avoidance persists!

Code


WindowWidth  =1000
WindowHeight = 700
UpperLeftX   =  50
UpperLeftY   =  50

graphicbox #john.g2, 350,  10, 606, 610

open "Statistics of last digits of primes." for window as #john

    #john "trapclose [quit]"

    #john.g2 "down ; fill cyan"

    topinteger =1000000

    dim bin( 10, 10)    '   actually need only 1, 3, 7, 9.......

[start]
    dim ints( topinteger)
    for j =1 to topinteger
        ints( j) =1
        scan
    next j

    for j =2 to 1 +topinteger^0.5
        if ints( j) =1 then gosub [strikeout]
        scan
    next j

for j =2 to topinteger
    if ints( j) =1 then
        'print j
        currLastDigit =last( j)
        bin( currLastDigit, oldLastDigit) = bin( currLastDigit, oldLastDigit) +1
        oldLastDigit  =currLastDigit
    end if
    scan
next j

'data 1, 3, 7, 9

for i =1 to 9
    for j =1 to 9
        print bin( i, j),
    next j
    print ""
next i

wait

function last( j)
    j$ =str$( j)
    last =val( right$(j$,1))
end function

[strikeout]
    call setxy, i

    for k =2 *j to topinteger step j
        ints( k) =0
        call setxy, k
    next k
return

sub setxy jf
    y =int( jf /600)
    x =jf -600 *y
    #john.g2 "set "; 2+x; " "; 2+y
end sub

[quit]
close #john
end