Presentation of 2D & 3D Datasets
Large data sets are hard for humans to see patterns & relationships, and slow for computers.
2D Data- d =f( x, y)
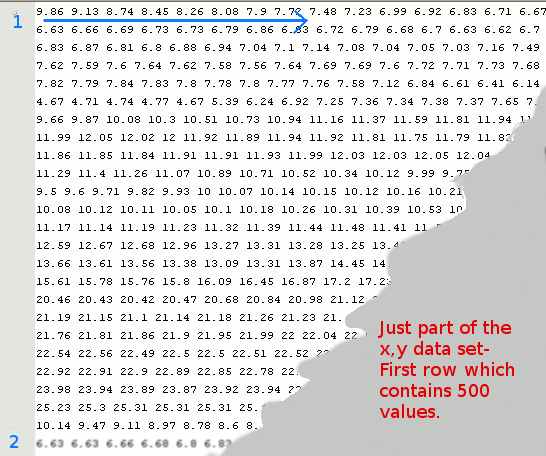
Can you guess what this dataset represents? Not without help.. but by all means download it and try your own 'visualisations'.
A typical 2D dataset might represent vegetation type; soil conductivity;
magnetic field intensity; ground-penetrating radar signal return; and
even ( occasionally!) elevation above a datum like sea-level. It may
represent isolated and unconnected values ( a sparse set)- say 'a church
is here'- or regularly spaced samples of a continuous distribution.
Closely related to things like lidar.
The data shown here is 250,000 values, measured on a 500x500 x/y grid.
Just looking at the numbers you have NO IDEA what they might represent.
Scanning by eye you can see neighbours have similar values, and get a
rough idea of max & min. Little else.
However there are ways to make it easier on the eye. One is to
colour-code the values. Here I've alrready 'cheated' since I had some
idea of max & min, and could therefore better use the colour range.
At the expense of some slowness, it is better to let the computer read
all the values & itself find min & max, then use the full colour
range possible- and a better palette.
It looks ( perhaps because of prior exposure to similar plots?) as if we
may be looking at some kind of surface, rather than randomly scattered
values. Can we plot it in a way that emphasises this possibility? One
possibility is as a pseudo-perspective view.
Mmm... Could that be a real hill at the top right? A valley snaking
towards us?? Perhaps a forking railway or road embankment??? The colour
range is being a bit confusing, and the lack of perspective and
real-time rotation don't help. And perhaps if it represents areal ground or tree-canopy surface I've got the data inverted???
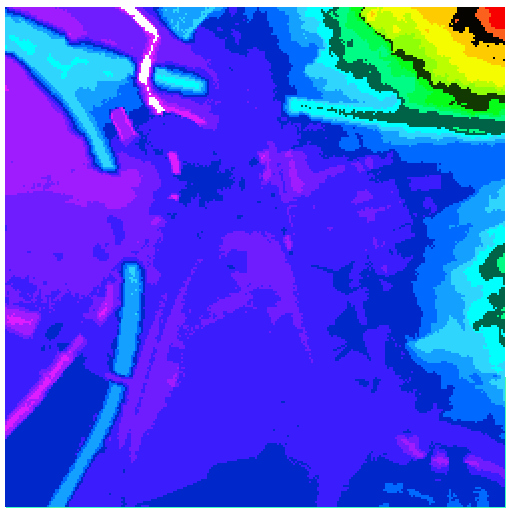
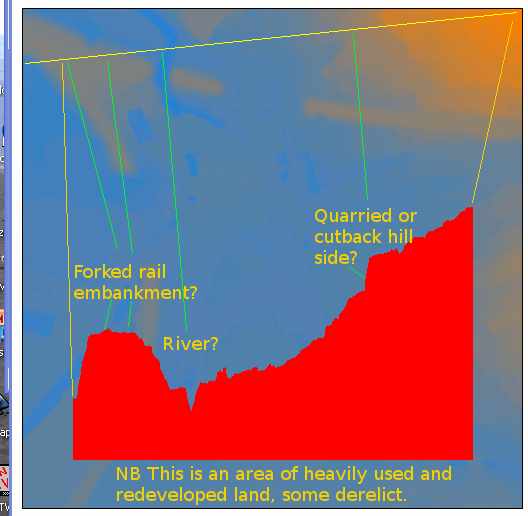
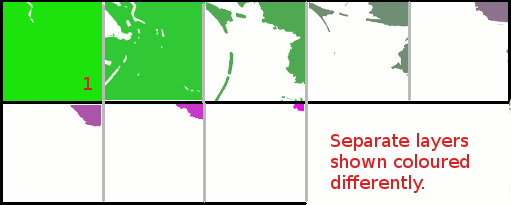
Another way of helping humans attempting to analse this same data is to allow cross-sections to be examined at will, as done for the following software version- or examine the layers side by side.
- 
I haven't yet tried writing a version to show an x/y 'net'. To be useful with such big datasets you'd need to either scroll across a VEY large image, or perhaps do in vector format like svg. Both do-able in LB.
By now we've a better idea of what is going on. I'll still not tell you
what the data represents- it could be ground elevation, but could also
be height of tree canopy top, or soil moisture or .....
3D Data d =f( x, y, z)
Now we have a dataset that associates a value with every location in 3D
space- sometimes called a voxel. The simplest case is for the data again
to be scalar.
A very important case might be atmospheric modelling. Data at each (xyz)
'voxel' would hold pressure, temperature, humidity etc as scalars or
vectors. Or a dataset could represent tissue type throughout a
whole-body CAT-scan. Or activity in your brain as you sit puzzling over Liberty BASIC! We may be interested in the 'surface' of a real 3D object, or the distribution of something within it.
-
-
A more specialised case is the limited 'point cloud' dataset
representing xyz coordinates of a surface, whether calculated or
scanned. There's a lot of amateur activity scanning small 3-D objects,
and commercially lidar is very important.
-
In all cases, it is MUCH preferable to have interactive ability to 'fly
in and around' the structures. The rotating torus requires fast,
compiled code to create in real time, so I cheated by showing someone
else's results. Failing that ( slow processing) build up an animated
GIF, as above right. The code used here in LB used ImageMagick to make
the animated GIF. It runs at about this speed, but in LB you see each
image frame being created, while in the animation you just see the
endpoint of each stage.
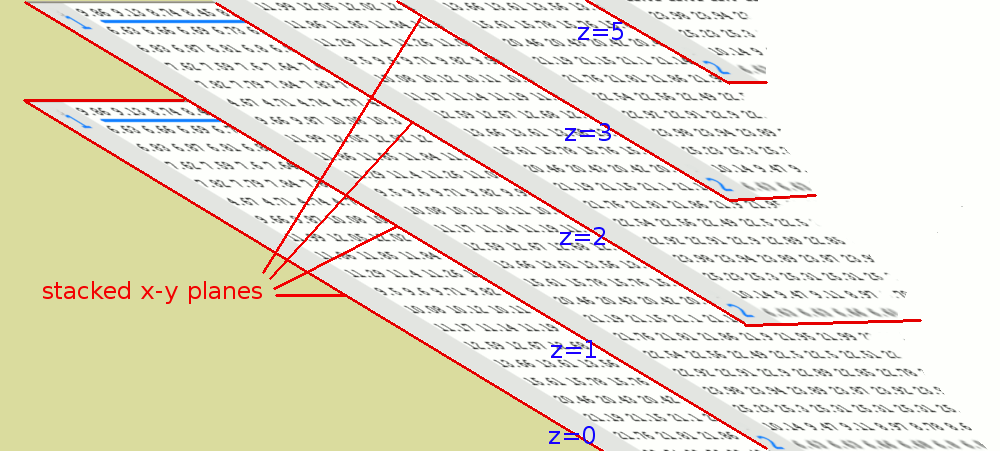
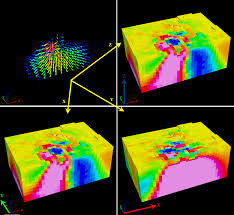
ImageMagick can be run from within LB or from the command line- 'convert -resize 200x200 -delay 200 *.bmp anim3D5.gif'.
PS Are you any clearer on what the 2D dataset represented? Look at http://www.bluesky-world.com/downloads/#
Code is available as download.
You may want to visit my other pages at Diga Me!