Linear equations- Gauss-Jordan matrix inversion

-

The following code asks for the terms of a square matrix & returns its inverse. The result is calculated by the Gauss-Jordan method, with corrections, as referenced from Wikipedia. Thanks Mr Kahan at Berkeley!
It also multiplies the matrix by the inverse to confirm the result.
Not tested above 3x3, but dimensioned for up to 10x10 ( & could go higher)

 ' Gauss-Jordan matrix inversion a => Inv( a)   GJ4.bas

 ' including checks for excessive growth despite row-pivoting,
 '       and adjustments for zero pivots to avoid 'division by zero' errors.

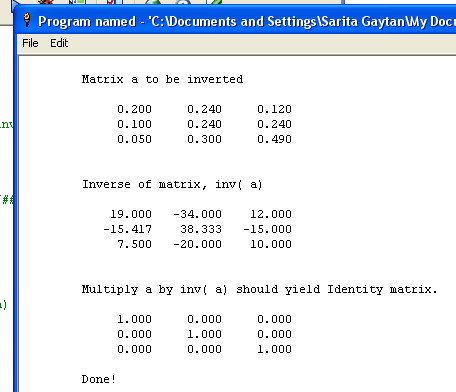
 '  As a check,  0.20    0.24    0.12    transposes ( approx.) to      19    -34     12
 '               0.10    0.24    0.24                                 -15.4   38.33 -15
 '               0.05    0.30    0.49                                   7.5  -20     10

 '  ... and these multiply correctly to the Identity matrix     1    0    0
 '                                                              0    1    0
 '                                                              0    0    1
 '             ... to a convincing ( ??) accuracy.

dim a( 10, 10), x( 10, 10), p( 10)  '   I choose to stay below 10x10 matrices
dim I( 10, 10)                      '   To check-calculate a times inv( a)

                                    ' first determine levels of roundoff and over /underflow.

ufl = 1e-20                         ' ... = max{ underflow, 1/overflow) thresholds.

g =4 : g =g /3 : g =g -1            ' ... = 1/3 + roundoff in 4/3
eps = abs( ((g +g) -1) +g )         ' ... = roundoff level.

g = 1                               ' ... will record pivot-growth factor

print ""
print "  Square Matrices only!"
print ""

input "  Number of rows /columns ( integer, >1 and <10) "; n

if n <>int( n) or n <2 or n >10 then wait

print ""
print "  Enter matrix elements:"

for i =1 to n
    for j =1 to n
        print " a( "; i; ", "; j;") = ";
        input a( i, j)
    next j
next i

cls

print ""
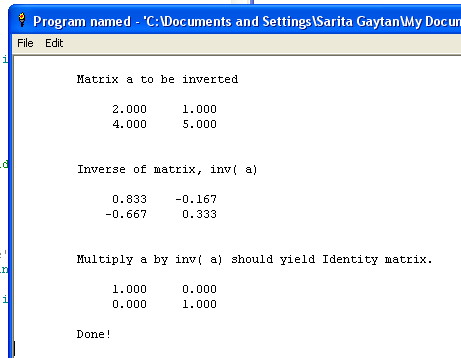
print tab( 10); "Matrix a to be inverted"       ' display looking like a matrix!
print

for i =1 to n
    for j =1 to n
        print tab( 5 +8 *j); using( "###.###", a( i, j)); "   ";
    next j
    print ""
next i

print

                                    ' copy a to x and record each column's biggest element.
for j =1 to n
    p( j)=0
    for  i =1 to n
        t        =a( i, j)
        x( i, j) =t
        t        = abs( t)
        if t >p( j) then p( j) =t
    next i
    '   print "Column "; j; " had max "; p( j)
next j

for k =1 to n                       ' ... perform elimination upon column k .
    q =0
    j =k                            ' ... search for kth pivot ...
    for i =k to n
        t =abs( x( i, k))
        if t >q then
            q =t
            j =i
        end if
    next i

    if q =0 then
        q =eps *p( k) +ufl
        x( k, k) =q
    end if

    if p( k) >0 then
        q =q /p( k)
        if q >g then g =q
    end if

    if g >8 *k then
        print "Growth factor g = "; g; " exceeds "; 8 *k; "; try"
        print "moving a's column "; k; " to col. 1 to reduce g."
        wait                                        ' ... or go back to re-order a's columns.
    end if

    p( k) =j                               ' ... record pivotal row exchange, if any.
    if j <>k then                          ' ... no need to swap if equal.
        for l =1 to n
            q        =x( j, l)
            x( j, l) =x( k, l)
            x( k, l) =q
        next l
    end if

    q        = x( k, k)
    x( k, k) =1

    for j =1 to n
        x( k, j) =x( k, j) /q
    next j

    for i =1 to n
        if i <>k then
            q        = x( i, k)
            x( i, k) =0
            for j =1 to n
                x( i, j) =x( i, j) -x( k, j) *q
            next j
    end if
    next i
next k

for k =n -1 to 1 step -1                            ' ... unswap columns of x
    j =p( k)
    if j <>k then
        for i =1 to n
            q        =x( i, k)
            x( i, k) =x( i, j)
            x( i, j) =q
        next i
    end if
next k

print
print tab( 10); "Inverse of matrix, inv( a)"
print

for i =1 to n
    for j =1 to n
        print tab( 5 +8 *j); using( "###.###", x( i, j)); "   ";
    next j
    print ""
next i

print ""
print ""
print tab( 10); "Multiply a by inv( a) should yield Identity matrix."
print ""

for i =1 to n
    for j =1 to n
        for index =1 to n
            'Dive' the matrix row down the inverse's column
            I( i, j) =I( i, j) +x( i, index) *a( index, j)
        next index
        print tab( 5 +8 *j); using( "###.###", I( i, j)); "   ";
    next j
    print ""
next i

print ""
print tab( 10); "Done!"
wait

end